Archimedes a detektoring
Neustále mnozí detektoráři narážejí na neskutečný problém, jak jednoznačně a bezpečně určit, z jakého materiálu asi je onen, zajisté v potu tváře, vyhrabaný poklad.
Archimédes (288 - 212 B. C.), jsa pověřen králem Hierónem II., aby ověřil množství zlata v zhotovené koruně, pak na řešení úkolu přišel ve vaně a nahý vyběhl na ulici s pokřikem : ,, Heuréka !"
My však naštěstí již nemusíme běhat nazí po návsi, ale můžeme v poklidu útulného domova s úspěchem využít právě tento Archimédův zákon.
Mnohdy se vedou nekonečné diskuze o tom, jak se s tímto problémem vypořádat.
Zde jsou některé z možností :
1.Zcela amatérské a tím velmi ošidné jsou různé babsko - hospodské rady :
a/zkouška psaním na papír (Pb, Ag a grafit zanechávají stopu). Zde je však počet prvků značně omezen, stopu zanechávají i různé slitiny s přiměsemi těchto kovů.
b/zkouška potěžkáním v ruce. Jde o způsob značně nejistý, často s chybným výsledkem, rozdíl měřených hmotnosti je zdánlivě dostatečný (Sn 8,0 - mosaz 8,5 - Ag 10,5 - Pb 11,34 - Au19,32 g/cm3). Opak je však pravdou. Viz úspěšné snahy rumunských čímanů s Au prsteny, právě, právě, právě teď nalezenými na zemi (jde však o mosaznou imitaci a veskrze uměleckou scénku nálezu prstenu). V tomto případě je rozdíl měrných hmotností značný (mosaz 8,5 g/cm3 ku 19,32 g/cm3 u zlata) a nepomůže ani přítomnost puncu (ten Vám leckterý zlatník za drobnou úplatu zhotoví na Vámi přinesený šperk, a to i na počkání - vlastní zkušenost). A přesto tito zlotřilci slaví úspěchy - což je potvrzením neúčinnosti této metody, jež se hodí tak akorát na potěžkávání králíků v holešovické tržnici.
c/zkouška ohněm, opálení zapalovačem. Zde má údajně docházet k rozdílnému stupni opálení kovů. Osobně jsem byl přítomen této vskutku obskurní metodě - samozřejmě naivní kupec byl celkem snadno pokoutní kuplířkou napálen.....
2. Výpočet měrné hmotnost (ze známého objemu tělesa a jeho hmotnosti). Jednoduchým algebraickým výpočtem ze vzorců pro tyto objemy. To však lze provést pouze u těles pravidelných tvarů (koule, krychle, válec). V případě slitin kovů je však metoda neúčinná - získáme pouze průměrnou měrnou hmotnost, ale procentní zastoupení jednotlivých kovů nezjistíme. Metoda je zároveň nepoužitelná pro artefakty členité, duté apod.
3. Měření objemu vytlačene kapaliny.
a/odebírání vody ze zkumavky pipetkou a její následně zvážení (po označení hladiny kapaliny před a po ponoření tělesa).
b/přelití kapaliny přes hranu zkumavky po vložení artefaktů (opět její následné zvážení).
Tyto metody mají však mnoha úskalí, vedoucí často k velkým chybám (v řádu až vyšších jednotek %). Jde jednak o přesnost vyznačených rysek na kádince, konkávní/konvexní hladinu vody v nádobce (danou povrchovým napětím kapaliny) a nepřesností při odebírání kapaliny pipetkou.
Obě metody jsou dosti amatérské, vhodné spíše pro produkci potulných šarlatánů.......
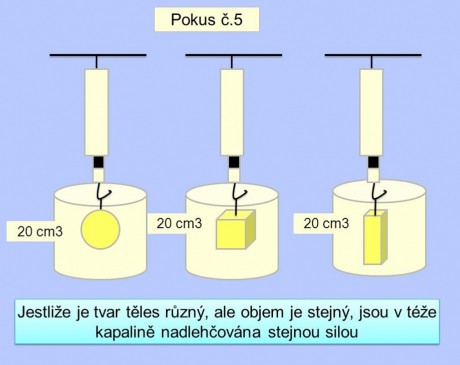
4. Přesnější metodou je jistě přímé využití Archimédova zákona (..... těleso ponořené do kapaliny je nadlehčováno silou, jež se rovná hmotnosti kapaliny tělesem vytlačené). A právě o tuto sílu nám zejména jde. K měření použijeme buď dvouramennou laboratorní váhu, či váhu mincovní (mincíř) nebo stolní digitální váhu - její cena je pouhých 120 Kč a prodává ji každý Číňan (POCKET SCALE - váživost 200g/0,01g). Postup měření vidíme v přidaných fotech.
Potřebujeme k tomu zátku z umyvadla (jako základnu), vteřinové lepidlo, silnější drátek na šibeničku, nit na zavěšení a kádinku s kapalinou. Po instalaci šibeničky na digitální váze její hmotnost (táru) vynulujeme. Artefakt zavěsíme na nit a závažíme (tzv. na sucho - ve vzduchu), poté přistrčíme nádobku a artefakt ponoříme zcela do vody. Na displeji váhy odečtememe obě hmotnosti a můžeme začít s výpočetem.
V = objem vytlačené vody je roven rozdílu vah při měření na sucho a ve vodě (protože měrná hmotnost vody ® =1g/cm3)
V = g1 - g2
m = hmotnost artefaktu (tzv. na suchu) - tedy g1
® = m/V = g1/(g1 - g2)
Metoda je velmi rychlá, nenáročná na vybavení, přesná (nehrozí jakákoliv ztráta kapaliny), jen je nutno zajistit, aby na povrch artefaktu neulpěly bublinky vzduchu. Zároveň nesmí artefakt obsahovat žádné dutiny (zdánlivě by zvětšovaly objem tělesa). Hmotnost nitě závěsu je zanedbatelná a můžeme ji pominout. Zároveň tak, jako v předchozím případě, nerozpoznáme skutečný podíl jednotlivých kovů v případě slitiny.
Je ovšem potřeba se vyhnout různým kuriózním způsobům měření (jak byly popisovány v komentářích na LP). Např. jeden z badatelů umístil kádinku s vodou na váhu, pak do ní vkládal artefakt a podivoval se, že nemá správný výsledek, jiný zase držíce artefakt na niti v ruce jej ponářel do kádinky umístěné na váze. A také je nutno znát aspoň základní fyzikální a matematické postupy u Archimédova zákona, jak jsme vypozorovali u badatele - lukegoss - ne vždy je to každému úplně jasné, ač jde o učivo pro žáky 7.třídy ZŠ a znalost těchto elementárních zákonitostí je pro zvládnutí pokusu zcela nezbytná.........
Některé z těchto metod jsou i popsány v článku na LP - čištění a konzervace (Elmara), kde však autor příspěvku článek tzv. obšlehl (t.j. i s chlupama) z práce jiného autora vč. gramatických a stylistických chyb, aniž by se obtěžoval označit citaci - tedy čistý plagiát......
1url.cz/XKMNW Lovec pokladů
Zde ona okopčená pdf - Jan Bukvic
1url.cz/SKMNi
Zde jen malá odbočka - nechť si každý tvoří plagiáty dle své libosti, to je mi vcelku lhostejné. Udivuje mne však, pokud jiné, tzv. autority poukazují na plagiátorství u druhých, ač použité zdroje uvedete... Proč tak činí.... ? Těžko říci - zda zloba, závist, či tzv. prostřelené ego. Na každý případ mi případne podobné jednán infantilní, hodící se tak akorát na dětské pískoviště.
Viz přílohy screenů ve fotogalerii.
5. Metodou jistě exaktní je pak využití spektrometru - používá se často i ve zlatnictvích - odpadá pak zkoušení ryzosti Au lučavkou královskou a buližníkem (zde ji na požádání - za úplatu můžeme využít). Metoda je nedestruktivní, rozpoznáme jednotlivé druhy prvků a jejich procentní zastoupení, nevadí případné dutiny v artefaktu, nejsou obtíže se ztrátou kapaliny, problémy s kovexností/konkávností hladiny kapaliny, či ulpívání vzduchových bublin na povrchu. Jedinou vadou je pak vyšší cena takového přístroje (od 10 000 do 240 000 Kč.) pro případné domácí použití. Jinak ovšem je tato metoda plně kredibilní....
Odkazy na podobné přístroje -
1url.cz/Szdv5
1url.cz/Vzds7
Příklad jednoho měření měrné hmotnosti - šatní závaží s hrazdičkou :
g1 =12,4g g2 =11,32
® = m/V =g1/(g1 - g2)
= 12,4/(12,4 - 11,32) = 11,48 g/cm3 (vypočtená měrná hmotnost)
Rozpoznáme tak, že měřený artefakt je čisté Pb a můžeme pak v komentářích dát určitější zjištění, než ono vágní - je to těžké, leskne se to - možná Ag a podobné neurčitosti, někdy i holé nesmysly.....
Jak vidíme, vypočtená m. h. se od tabulkové hmotnosti liší (11,34g/cm3)
Zjištění absolutní chyby měření -
©% = 11,48/0,1134 = cca 1,24 %
Chyba se zdá vcelku malá a zanedbatelná, ovšem při vážení ještě o něco drobnějších předmětů její hodnota propočtená potom jako relativní chyba měření roste a výsledky pokusu znehodnocuje....
Zde ještě údaje o měrné hmotnosti některých kovů, kde se setkáváme nejčastěji s nejasnostmi :
Cu 8,96
mosaz 8,4 - 8,75
Ag 10,5
Pb 11,34
Au19,32
Všechny údaje samozřejmě jako g/cm3.....
Zde tabulka pro některé prvky :
1url.cz/Fz1V5
Na dalších odkazech pak něco o Archimédově zakonu
1url.cz/pKtWW
A něco o mechanice tekutin
1url.cz/MKtWo
Na dalším odkazu pak potvrzení neznalostí páně - lukegoss - týkající se Archimédova zákona -
1url.cz/YKtW1 - "Pb placka"
Obává se, že Au a Fe vytlačí stejné množství kapaliny a že to má být na závadu pokusu...
Jistě ano, vytlačí stejné množství kapaliny, je však nezbytné tyto artefakty jednotlivě předem zvážit pro zjištění údajů g1 (viz pokus výše ). Zároveň i neznalost fyzikálních zákonitostí -
1kg jakéhokoliv kovu (prvku, slitiny) =1kg vytlačené vody
Můžeme potom s podivem pozorovat jak se nám tento badatel holedbá svými znalostmi v oboru matematiky (výpočty příhradových nosníků - viz screen a odkaz)
1url.cz/BzlOo LP - "RITA 30 E/E"
Nejen, že to zavání (resp. silně zapáchá samochválou), ale je i v protikladu s predchozím tápáním... Osobně bych si od takového badatele nenechal spočítat ani nosníky do králikárny.....
Pozoruhodné - snad jemu a i podobným zoufalcům, tato edukativní vložka aspoň trochu pomůže orientovat se v dané problematice.....
Na nižším odkazu
1url.cz/0KtWL "příroda si hraje" - LP
Zde můžeme pozorovat, jaké obtíže při pokusu představuje, když používáme kuchyňské nádobí a s tím i doprovodné chyby měření - zachytávání vytlačené vody.....
Další z obtíží při použití Archimédova zákona je, když oveřujeme slitiny např. Ag, či Au kovů (resp. kovy s různou úrovní ryzosti).
Bilon : kov na mince 50/50 %
měrná hmotnost
Ag - 10,5 g/cm3
Cu - 8,96 g/cm3
Výsledná průměrná hmotnost je pak 9,73g/cm3 - musíme pak podle tabulky v práci J. Bukvice vyhledat příslušný kov....
Obdobně u zlata :
Au-19,32 g/cm3
Cu - 8,96 g/cm3
Výsledná měrná hmotnost - 14,14 g/cm3
Ani případný punc, jak jsme si již přečetli výše, tak není zárukou ryzosti, data musíme při měření odečítat z tabulky a tak se jeví jedinou správnou a bezchybnou metodou použití spektrometru a námi naznačenou metodu Archimédova zákona používat pouze jako doplňkovou....
Náhledy fotografií ze složky Archimedes a detektoring